まずは福利運用とは何かを確認しておきましょう
単利と福利の違い
例えば、今100万円持っていて、年利2%で運用した場合の5年後の金額は?
単利の場合
1.000.000円 × 2% = 20.000円
20.000円 × 5年 = 100.000円
1.000.000円 + 100.000 = 1.100.000円
単利の場合は最初の元本100万円に対してついた利子2万円が
毎年単純に増えていく計算になります。
毎年同じ利子がついていくのが福利です。
福利の場合
①1年目 1.000.000円 × 2% = 20.000円 ➡ 1.020.000円
②2年目 1.020.000円 × 2% = 20.400円 ➡ 1.040.400円
③3年目 1.040.400円 × 2% = 20.808円 ➡ 1.061.208円
④4年目 1.061.208円 × 2% = 21.224円 ➡ 1.082.432円
⑤5年目 1.082.432円 × 2% = 21.668円 ➡ 1.104.100円
福利の場合は最初の元本100万円に対してついた利子2万円が
元本に加算されて2年目は102万円に対しての利息が2%つくことになります。
このように毎年加算された元本に対して利子がつくのが福利運用です。

アインシュタインが福利を「人類最大の発明」と言ったそうです。
時間が経つにつれ、どんどん元本と利子が増えていくのが
想像できますね。
6つの係数の考え方
期間5年の場合の係数表
※係数表は資料として試験に出されますので、数字を覚える必要はありません。
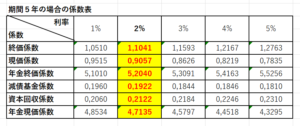
今100万円持っていて、年利2%で運用した場合の5年後の金額は?
これは終価係数を用いて計算することになります。
1.000.000円 × 1.1041 = 1.104.100円
※ 2%で5年福利運用なので、1.02×1.02×1.02×1.02×1.02 = 1.1041
要は、今ある金額を福利運用した一定期間後の金額を求める時に用いるのが
終価係数です。
どの係数を使えばいいのかわからなくなった場合も、焦る必要はありません!
5年運用すれば絶対に金額が減ることはないことが前提なので、表の中の
0,9057、0,1922、0,2122という係数は、 掛け算すると金額が減ってしまうので、
ここでは必年的にありえないですよね。
逆に、5,2040、4,7135という係数は、掛け算すると金額が増えすぎです。
2%の利子で5年運用すれば、係数的には1,1041という係数が理にかなっていると
わかると思います。
年利2%で5年後に100万円を用意するのに、元本はいくら必要?
これは現価係数を用いて計算することになります。
1.000.000円 × 0.9057 = 905.700円
要は、一定期間後に一定金額に達するために必要な元本を求める時に用いるのが
現価係数です。
解説
5年運用して100万になるということは、元本金額は減ることが前提です。
ですので、表の中の1,1041、5,2040、4,7135という係数は、掛け算すると
金額が増えてしまうので、ここでは必年的にありえません。
逆に、0.1922、0.2122という係数は、掛け算すると金額が減りすぎです。
2%の利子で5年運用して100万円になるということは、係数的には
0.9057という係数が理にかなっているとわかると思います。
年利2%で毎年20万円を5年間積み立てた場合の5年後の金額は?
これは年金終価係数を用いて計算することになります。
200.000円 × 5.2040 = 1.040.800円
要は、毎年一定金額を積み立てた場合の、一定期間後の元利合計を求める時に
用いるのが年金終価係数です。
解説
毎年20万円を5年間運用しながら積み立てるのですから、金額は少なくとも
100万以上になるということが前提です。
ですので、表の中の5,2040以外の係数は、掛け算すると金額が100万より
減ってしまうので、ここでは必年的にありえません。
5.2040という係数が理にかなっているとわかりますね。
年利2%で5年後に100万円を用意するには、毎年いくらの積み立てが必要?
これは減債基金係数を用いて計算することになります。
1.000.000 × 0.1922 = 192.200円
要は、一定期間後に一定金額を用意するための、毎年の積立金額を求める時に
用いるのが減債基金係数です。
解説
毎年5年間積み立てて100万円になるのですから、2%運用してない場合は
毎年20万円積み立ててることになります。この場合の係数は20万÷100万で
0.2になりますが、2%利子がつきながら運用しているので、係数は0.2より少し
少ない数字になります。ですので、表の中の0.1922以外の係数は、ここでは必年的にありえません。
0.1922という係数が理にかなっているとわかります。
100万円を年利2%で運用しながら5年間で取り崩した場合の毎年の受け取り額はいくらか?
これは資本回収係数を用いて計算することになります。
1.000.000 × 0.2122 = 212.200円
要は、現在の一定金額を一定期間で取り崩した場合の、毎年の受け取り金額を 求める時に用いるのが資本回収係数です。
解説
2%運用してない場合は、100万÷5年で毎年20万円受け取ることになり、
この場合の係数は20万÷100万で0.2になります。
ですが、2%利子がつきながら運用しているので、係数は0.2より少し大きい
数字になります。ですので、表の中の0.2122以外の係数は、ここでは必年的に
ありえません。
0.2122という係数が理にかなっているとわかります。
5年間にわたって20万円ずつ受け取る場合、年利が2%だと、必要な元本はいくらか?
これは年金現価係数を用いて計算することになります。
200.000円 × 4.7135 = 942.700円
要は、将来の一定期間にわたって一定金額を受け取るための必要な元本金額を 求める時に用いるのが年金現価係数です。
解説
2%運用してない場合は、20万円を5年間受け取るために元本は100万円
必要になり、100万÷20万で、この場合の係数は5になります。
ですが、2%利子がつきながら運用しているので、係数は5より少し小さい
数字になります。ですので、表の中の4.7135以外の係数は、ここでは必年的に
ありえません。
4.7135という係数が理にかなっているとわかります。
言葉のキーワードでおぼえる場合

減債基金係数だけ覚えておけば、他の係数は
終価・現価・回収のキーワード言葉で何とかなります。
終価 ➡ 一定期間後の金額を求める問題
※終価係数 (毎年運用した期間後の金額)
※年金終価係数 (毎年運用しながら積み立てた期間後の金額)
現価 ➡ 元本を求める問題
※現価係数 (必要な元本を求める係数)
※年金現価係数 (取り崩す時に必要な元本を求める係数)
回収 ➡ 受け取り額を求める問題
※資本回収係数 (受け取り = 回収)
減債基金係数だけ、毎年の積立額を求める問題なことを覚えておきましょう。


コメント